22
Cientistas
da Nasa recalculam idade da estrela mais velha já descoberta
Cientistas da agência espacial
americana (Nasa) recalcularam a idade da estrela
mais velha já descoberta,
conhecida como “Estrela Matusalém” ou HD 140283. Eles
estimam que a estrela possua 14,5
bilhões de anos, com margem de erro de 0,8
bilhão para menos ou para mais, o
que significa que ela pode ter de x a y bilhões de anos.
De acordo com as informações do
texto, a soma x + y é igual a:
(A) 13,7
(B) 15,0
(C) 23,5
(D) 29,0
SOLUÇÃO COMENTADA:
Essa não tem nem muito o que comentar, é só fazer conta:
X = 14,5 – 0,8 = 13,7
Y = 14,5 + 0,8 = 15,3
X + Y = 13,7 + 15,8 = 29,0
RESPOSTA : D
23
Considere uma placa retangular ABCD de acrílico, cuja diagonal AC mede 40 cm. Um estudante,
para construir um par de esquadros, fez dois cortes retos nessa placa nas direções AE e AC, de
modo que DÂE = 45º e BÂC = 30º, conforme ilustrado a seguir:
Após isso, o estudante descartou a parte triangular CAE, restando os dois esquadros.
Admitindo que a espessura do acrílico seja desprezível e que raiz3 = 1,7, a área, em cm²
, do triângulo CAE equivale a:
(A) 80
(B) 100
(C) 140
(D) 180
SOLUÇÃO COMENTADA:
Vamos calcular a área dos triângulos ABC e ADE para subtrair da área do retângulo, mas para isso precisamos calcular o valor de cada lado:
Observando o triângulo ABC, temos
AB/40 = cos30° .:. AB = 40 1,7/2 = 34 cm
e temos
BC/40 = sen30° .:. BC = 40 1/2 = 20 cm
observando o retângulo, vemos que
BC = AD = DE (essa última relação de igualdade é válida pois o ângulo é de 45°)
Agora é só calcular as áreas:
RETÂNGULO = 20 x 34 = 680cm²
TRIÂNGULO(ABC) = 20 x 34/2 = 340cm²
TRIÂNGULO(ADE) = 20 x 20 /2 = 200cm²
TRIÂNGULO(AEC) = 680 - 340 -200 = 140 cm²
RESPOSTA LETRA C
24
Uma farmácia recebeu 15 frascos de um remédio. De acordo com os rótulos, cada frasco contém
200 comprimidos, e cada comprimido tem massa igual a 20 mg.
Admita que um dos frascos contenha a quantidade indicada de comprimidos, mas que cada um
destes comprimidos tenha 30 mg. Para identificar esse frasco, cujo rótulo está errado, são
utilizados os seguintes procedimentos:
• numeram-se os frascos de 1 a 15;
• retira-se de cada frasco a quantidade de comprimidos correspondente à sua numeração;
• verifica-se, usando uma balança, que a massa total dos comprimidos retirados é igual a 2 540 mg.
A numeração do frasco que contém os comprimidos mais pesados é:
(A) 12
(B) 13
(C) 14
(D) 15
SOLUÇÃO COMENTADA:
Considerando que todos os frascos contenham 20mg, o total que teriam na balança ao somar todos a massa de todos os comprimidos seria igual, a soma de uma PA de razão 20:
Sn = (20 + 300)15/2 = 2400
Mas como existe um termo (n) que é multiplicado por 30 e não por 40, daí, temos que
2400 - 20n + 30n = 2540
10n = 2540 - 2400
n = 14
RESPOSTA LETRA C
25
Uma máquina possui duas engrenagens circulares, sendo a distância entre seus centros A e B igual
a 11 cm, como mostra o esquema:
Sabe-se que a engrenagem menor dá 1000 voltas no mesmo tempo em que a maior dá 375
voltas, e que os comprimentos dos dentes de ambas têm valores desprezíveis.
A medida, em centímetros, do raio da engrenagem menor equivale a:
(A) 2,5
27
(B) 3,0
(C) 3,5
(D) 4,0
SOLUÇÃO COMENTADA:
Primeira informação R1 + R2 = 11
Depois sabemos que 1000x2piR2= 375x 2piR1 .:. daí temos 1000R1= 375R2
ele quer saber quanto vale R2, logo podemos escrever R1 = 110 - R2
e substituimos na segunda equação:
1000R2 = 375(11 - R2)
1000R2 = 4125 - 375R2
1000R2 + 375R2 = 4125
1375R2 = 4125
R2 = 4125/1375
R2 = 3cm
RESPOSTA LETRA C
26
Em uma sala, encontram-se dez halteres, distribuídos em cinco pares de cores diferentes. Os
halteres de mesma massa são da mesma cor. Seu armazenamento é denominado “perfeito”
quando os halteres de mesma cor são colocados juntos.
Nas figuras abaixo, podem-se observar dois exemplos de armazenamento perfeito.
Primeiro vamos ver quantas possibilidades ao acaso temos de conseguir uma arrumação perfeita;
como cada cor deve ficar devidamente ao lado do seu par, para a arrumação ser perfeita, temos:
10 x 1 x 9 x 1 x 8 x 1 x 7 x 1 x 6 x 1 = 30240
dividido pelo número de elementos repetidos que é 2 x 2 x 2 x 2 x 2 = 32
30240/32 = 945
Logo as chances de cair arrumadinha é de 1/945
SOLUÇÃO LETRA B
27
Um feirante vende ovos brancos e vermelhos. Em janeiro de um determinado ano, do total de
vendas realizadas, 50% foram de ovos brancos e os outros 50% de ovos vermelhos. Nos meses
seguintes, o feirante constatou que, a cada mês, as vendas de ovos brancos reduziram-se 10%
e as de ovos vermelhos aumentaram 20%, sempre em relação ao mês anterior.
Ao final do mês de março desse mesmo ano, o percentual de vendas de ovos vermelhos, em
relação ao número total de ovos vendidos em março, foi igual a:
(A) 64%
(B) 68%
(C) 72%
(D) 75%
SOLUÇÃO COMENTADA:
Vamos chamar o total de ovos de X no mês de Janeiro.
Então no primeiro mês 50% de X foram de ovos brancos e 50 % de X foram de ovos vermelhos.
Com isso sabemos que X/2 são ovos vermelhos e X/2 são ovos brancos.
No mês de fevereiro (2º mês) a quantidade de ovos brancos reduziu 10%, então passou a ser:
X/2 -10% de X/2 que é X/2 -X/20 = 9X/20
No mês de março, a quantidade de ovos brancos reduziram-se mais 10%, portanto, passaram a ser:
9X/20 - 10% de 9X/20 = 9X/20 - 9X/200 = 81X/200 - esse passa a ser o total de ovos branco no mês de março.
Agora vamos analisar o que aconteceu com os ovos vermelhos:
Em fevereiro:
X/2 + 20% de X/2 = X/2 + X/10 = 3X/5
Em março:
3X/5 + 20% de3X/5 = 3X/5 + 3X/25 = 18X/25 - total de ovos vermelhos no mês de março.
Total de ovos vendidos no mês de março equivale á 81X/200 + 18X/25 = 225X/200 = 9X/8
Então usando uma regrinha de 3 :
9X/8 -- 100%
18X/25 -- ?
? = 100 . 18X/25 .8/9X = 64%
RESPOSTA É LETRA A
28
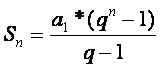 onde Sn = 40 000
onde Sn = 40 000
a1 = 1 e q = 2
daí vem a equação exponencial:
40 000 < 2^n - 1
2^n > 40 000
Vamos chamar o total de ovos de X no mês de Janeiro.
Então no primeiro mês 50% de X foram de ovos brancos e 50 % de X foram de ovos vermelhos.
Com isso sabemos que X/2 são ovos vermelhos e X/2 são ovos brancos.
No mês de fevereiro (2º mês) a quantidade de ovos brancos reduziu 10%, então passou a ser:
X/2 -10% de X/2 que é X/2 -X/20 = 9X/20
No mês de março, a quantidade de ovos brancos reduziram-se mais 10%, portanto, passaram a ser:
9X/20 - 10% de 9X/20 = 9X/20 - 9X/200 = 81X/200 - esse passa a ser o total de ovos branco no mês de março.
Agora vamos analisar o que aconteceu com os ovos vermelhos:
Em fevereiro:
X/2 + 20% de X/2 = X/2 + X/10 = 3X/5
Em março:
3X/5 + 20% de3X/5 = 3X/5 + 3X/25 = 18X/25 - total de ovos vermelhos no mês de março.
Total de ovos vendidos no mês de março equivale á 81X/200 + 18X/25 = 225X/200 = 9X/8
Então usando uma regrinha de 3 :
9X/8 -- 100%
18X/25 -- ?
? = 100 . 18X/25 .8/9X = 64%
RESPOSTA É LETRA A
28
Em um recipiente com a forma de um paralelepípedo retângulo com 40 cm de comprimento, 25 cm
de largura e 20 cm de altura, foram depositadas, em etapas, pequenas esferas, cada uma com
volume igual a 0,5 cm³. Na primeira etapa, depositou-se uma esfera; na segunda, duas; na
terceira, quatro; e assim sucessivamente, dobrando-se o número de esferas a cada etapa.
Admita que, quando o recipiente está cheio, o espaço vazio entre as esferas é desprezível.
Considerando 2^10= 1 000, o menor número de etapas necessárias para que o volume total de
esferas seja maior do que o volume do recipiente é:
(A) 15
(B) 16
(C) 17
(D) 18
SOLUÇÃO COMENTADA:
Vamos primeiro calcular o volume do paralelepípedo:
Vp = 40 x 25 x 20 = 20000 cm³
se cada esfera tem um volume Ve = 0,5, precisamos de um total de esferas igual á
Ne = 20000/0,5 = 40 000.
Temos uma PG de razão 2, nota-se (1,2,4,...)
Queremos saber quando a soma do número de termos dessa PG é igual ao total de bolinhas.
sabendo que a soma dos termos de uma PG finita é dado por:
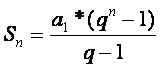
a1 = 1 e q = 2
daí vem a equação exponencial:
40 000 < 2^n - 1
2^n > 40 000
mas se 2^10 = 1000
temos
2^15 = 2^5x2^10 = 32000 ainda é pouco
2^16 = 2^6x2^10 = 64000 OPA! passou, então é esse aí!
RESPOSTA LETRA B

Gostei muito vc resolveu de uma forma mais simples.
ResponderExcluirespero em breve\o conseguir resolver exercícios comk estes desta forma!
Que, bom que eu ajudei.
ResponderExcluirE desculpe só lhe responder agora. Havia desativado o blog e só estou retomando agora.
Abráácos!